Siente la fuerza (Parte II)

Qué encontrarás en esta entrada?

• Cinemática basada en los sensores Android.
• Frecuencias electromagnéticas. 

En la última entrada os hablamos de AndroSensor y de cómo manipular los datos que este software nos permite guardar. Hoy vamos a comentar algunos de los resultados que he obtenido utilizando varios métodos para intentar ajustar estos sensores a la realidad física.

El Círculo:

Lo primero que vamos a hacer es dibujar un círculo a mano alzada con el móvil, y nos vamos a centrar, como la última vez, en la parte de la cinemática (análisis de la aceleración para intentar reconstruir la trayectoria). El algoritmo de diferencias finitas que utilizo ya fue esbozado en la entrada anterior, por lo que hoy nos vamos a dedicar a ver dibujitos.

Vemos la trayectoria tal cual sale de las lecturas del sensor:

Datos sin correcciones

Bien en verdad que a mi los círculos a mano alzada no se me dan muy bien... pero quizás éste haya salido especialmente mal.

El siguiente paso sería suponer que los acelerómetros estuviesen afectados por un error constante, un "error de cero", así que los intentamos ajustar para que el error sea compensado, obteniendo lo siguiente:

Datos con correcciones de cero para la aceleración

Supongo que habrá controversia al respecto... pero yo diría que lo de arriba se parece ya bastante a un círculo (al menos, a uno de los que dibujo yo a mano alzada).

Una cosa que se me ha ocurrido recientemente, es descartar las pequeñas vibraciones: ¿Qué pasaría si, en lugar de corregir la aceleración forzándola para que la velocidad sea nula al principio y al final, simplemente la "simplifico"?, y con "simplificar" me refiero a "cuantizarla". Defino un "paso mínimo", y obligo a la aceleración a que tome sólo valores que sean múltiplos enteros de esa "unidad" que acabo de definir. Con todo esto, obtenemos:

Datos con la aceleración cuantizada en pasos de 1m/s²

Bueno, también tiene pinta de círculo. Sin embargo, tiene un fallo importante:

Avance de la hélice en la dirección perpendicular al círculo

En el eje perpendicular al círculo, donde debería estar inmóvil, se mueve nada más ni nada menos que ¡¡4 metros!! No es un círculo, sino una especie de hélice que va avanzando.

El mismo problema lo presentaba la primera gráfica, asociada a datos en bruto, sin ningún tipo de corrección. Sin embargo, no era así cuando obligábamos a la velocidad a ser cero al inicio y al final.

Avance en la dirección perpendicular con la corrección de cero en la aceleración: aunque no sea nulo, éste es "sólo" de metro y medio

Avance en la dirección perpendicular sin correcciones: se dispara hasta los cuatro metros

La última idea es mezclarlo todo: ¿qué pasaría si cuantizamos la aceleración, y al mismo tiempo intentamos corregir el posible error de cero?

Aceleracioes con corrección de cero y cuantización en bloques de 1m/s²

La hélice avanza, pero menos que en cualquiera de los casos anteriores

En este último caso obtenemos un círculo (si bien es verdad, que algo "chuchurrío"), y el avance en la dirección perpendicular es "sólo" de metro y medio. En realidad este "avance" debería ser casi nulo (20cm a lo sumo), pero es el mejor resultado que he obtenido hasta el momento.

A continuación, vamos a ver las gráficas de la cinemática en los dos casos más favorables. La posición está en azul, la velocidad en rojo, y la aceleración en verde. Al terminar el trazado del círculo en el mismo punto en el que lo empezamos, ambas deberían acabar en cero, pero vemos que en ambos casos acaban en metro y medio.

Posición, velocidad y aceleración en la dirección del trazado sin cuantizar la aceleración

Posición, velocidad y aceleración en la dirección del trazado cuantizando la aceleración

En la segunda gráfica se puede apreciar la cuantización de la aceleración. Ésta sólo puede valer múltiplos enteros de 1m/s² (1m/s², 2m/s², 3m/s², ...).

A continuación, dibujamos las gráficas de los casos más desfavorables: aquellos en los que no hemos corregido el error de cero de la aceleración, desviándose notablemente en la dirección perpendicular:

Sin corrección de cero ni cuantizado

Sin corrección de cero, pero con la aceleración cuantizada

Paradójicamente, si nos fijamos sólo en la dirección del trazado, estos círculos empezaron en el mismo punto donde acabaron, lo cual es correcto. El problema es que los valores para el eje perpendicular al trazado son completamente irreales.

En cualquier caso, y aunque aún hay mucho en lo que mejorar, de momento me quedo satisfecho en lo que al dibujo de círculos se refiere... ¿y si lo intentamos con algo más complicado?

El Corazón:

Partiendo de lo anterior, dibujo los cuatro corazones:

Sin corrección de cero ni cuantizado

Con corrección de cero, pero sin cuantizado

Sin corrección de cero, pero con aceleraciones cuantizadas

Con corrección de cero y aceleraciones cuantizadas

Como si de una constante se tratara, en los casos en los que no hemos corregido el error de cero en la aceleración se desvían unos cuatro metros en la dirección perpendicular, mientras que en los que sí lo hemos corregido, el desvío es de metro y medio. En este caso, si tuviera que elegir el que más se parece a la realidad, creo que me quedaría con el segundo. Sin embargo, el segundo no tiene las aceleraciones cuantizadas, y eso puede dar problemas, como veremos en el siguiente caso.

El caso estático:

Vamos a dejar el móvil quieto encima de la mesa, y a ver qué pasa...

"Trayectoria" de un móvil parado con datos en bruto

La conclusión es indiscutible: el móvil se teletransporta a través de dimensiones ocultas del espacio y, aunque parezca que no se mueva de encima de la mesa, recorre unos 80 metros en su apasionante viaje lleno de misterios a través de la parafísica... Bueno, puede ser eso, o que los sensores se hayan visto afectados por un importante error que se potencie con el tiempo.

Vamos a ver cómo se comporta nuestro móvil parado con las distintas correcciones en la aceleración:

"Trayectoria" de un móvil parado con aceleraciones corregidas (error de cero)

"Trayectoria" de un móvil parado con aceleraciones cuantizadas

En el primer caso, la compensación del error de cero no es suficiente para "parar" al objeto, aunque sí acorta su viaje: en este caso pasa de los 80 a los 4 metros recorridos.

En la segunda gráfica (aceleraciones cuantizadas), no es que tengáis mala vista, sino que sólo se representa un punto y, al no estar en compañía de otros, es invisible. La posición del objeto está siempre en el origen. El objeto, por fin, se ha quedado parado.

En mi script he dejado todas las opciones programadas y accesibles, y seguiré trabajando en ello, pero parece que las mejores soluciones las aportan los métodos en los que corregimos el error de cero de la aceleración, siendo en algunos casos especialmente interesante añadir además el proceso de la cuantización.

Magnetismo:

Hasta ahora nos habíamos centrado en las variables cinemáticas, básicamente, en el estudio de la aceleración para reconstruir la velocidad y trayectoria del objeto en cuestión. Sin embargo, AndroSensor ofrece otras variables interesantes, como es el caso del campo magnético.

Bajando el otro día en mi ascensor me di cuenta de la variación tan pintoresca que tenía el campo a medida que bajaba.

He leído un poco por encima sobre el tema y, por lo visto, el hormigón del que están hechas las paredes de mi casa no es demasiado saludable de cara a las posibles interferencias electromagnéticas. De hecho, según Radiansa, la normativa española establece como límite 100 microteslas para campos magnéticos de 50Hz.

En este caso medimos campos que pasan de los 60 microtestas, aparentemente estacionarios (aunque no sé si realmente se está midiendo el promedio temporal de un campo oscilante de más alta frecuencia). La modulación que se observa proviene del movimiento del sensor (que está bajando en un ascensor), de tal manera que lo que estamos viendo es una variación en el espacio, y no en el tiempo.

Es interesante ver que entre piso y piso la amplitud del campo decae incluso casi media centena de microteslas. Se puede utilizar esto para ver claramente que en el recorrido del ascensor hemos cruzado ocho suelos, y así contar los pisos.

Afinamos un poco más este tipo de medidas, e incorporamos a nuestro script de análisis de datos de los sensores la funcionalidad de contar oscilaciones: por separado las bajadas y las subidas.

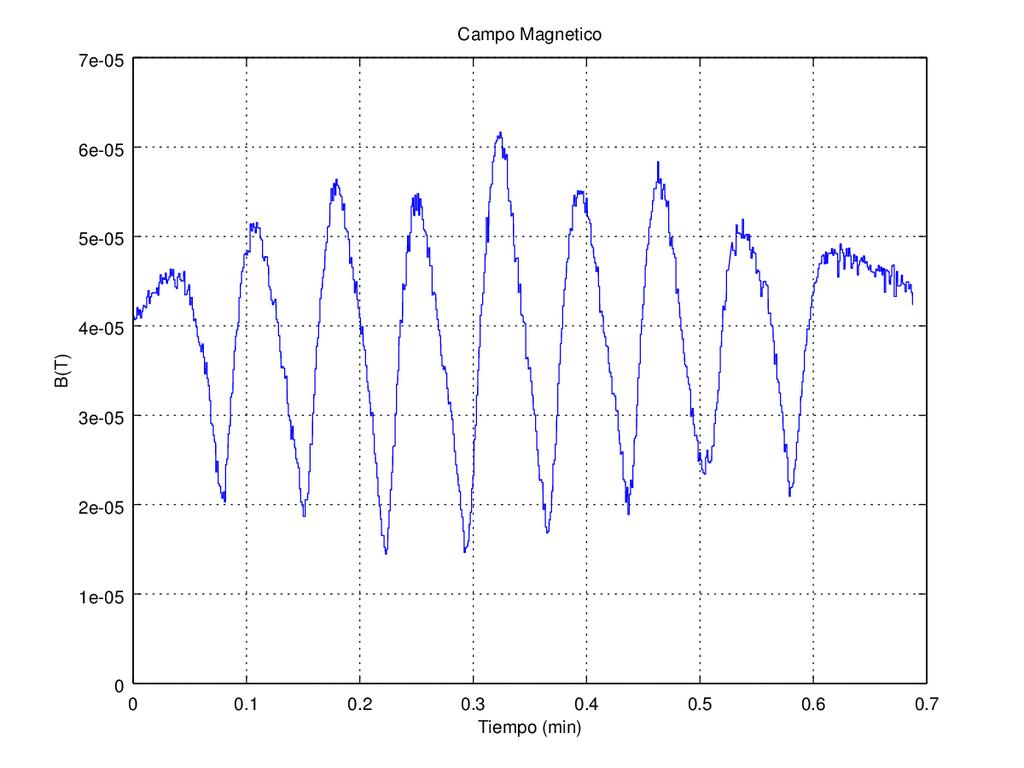
En este segundo experimento estamos viendo la señal con el sensor fijo. Se trata de uno de los casos estáticos de los cuales hemos estudiado la cinemática unas líneas más arriba. En esas circunstancias, estamos viendo la variación del módulo del campo magnético con el tiempo.

Viendo cuánto oscila a lo largo del tiempo medido, contamos que decae 379 veces, y que vuelve a subir otras 379 en unos 108 segundos. Eso da una frecuencia de unos 3'5 Hz. En general, en esa zona de mi habitación estoy midiendo frecuencias que van desde los 3 a los 4 Hz (bajas frecuencias). Insisto que no sé si se trataría de una frecuencia normal o, en el caso de estar midiendo promedios temporales del campo magnético, una frecuencia secundaria de modulación de la onda.

Informe Remoto:

Para finalizar, os comentaré la integración de este script en Astaroth's Bot System (ABSys), el sistema que me permite la comunicación con mi ordenador vía Hangouts.

Actualmente, puedo depositar los datos adquiridos con mi móvil en una carpeta en la nube que se sincroniza con una carpeta local de mi equipo de sobremesa. Una vez estén los datos en casa, dando una orden vía Hangouts, recibo el resumen del análisis por mensajería instantánea y al correo, incluyendo las gráficas en este último caso.

Un ejemplo curioso de integración entre Android, mensajería instantánea, shell de Linux y MATLAB/OCTAVE.