Con "A" de acelerómetro

Qué encontrarás en esta entrada?

• Revisión del problema de reconstruir la trayectoria partiendo de los datos de un acelerómetro.
• Ideas para reducir el ruido en las medidas.
• Gráficas de letras dibujadas a partir de lo anterior. 

Siguiendo el espíritu de la serie "Siente la fuerza" que escribí en este blog hace más de tres años (en especial la parte II), y dado que ayer Science Journal me hizo recordar lo mucho que añoraba a AndroSensor, no he podido resistirme a desempolvar mis torpes artes en MATLAB/OCTAVE y volverle a dar una vuelta al problema de cómo reconstruir la trayectoria mediante el acelerómetro.

Ya adelanto que no he conseguido más de lo que conseguí entonces. Mi conclusión hasta el momento - a no ser que alguien me convenza de lo contrario - es que es imposible obtener un buen resultado. Sin embargo, por el camino puedes ir haciendo cosas chulas.

La dificultad radica en el ruido de fondo que va recogiendo el sensor, y en que hay que integrar dos veces de manera numérica para llegar al resultado, el cual se construye, paso a paso, error sobre error, lo que termina siendo catastrófico.

Mis intentos de abordar el problema están relacionados con hacer correcciones en los datos que intenten limpiar ese ruido. En el script que me he hecho hoy, he contemplado las siguientes soluciones:

• Reducir la sensibilidad (desechando valores bajos de la aceleración).

• Corregir un posible error de cero (desplazar los datos para que cuando el objeto esté en reposo, no sienta ninguna aceleración).

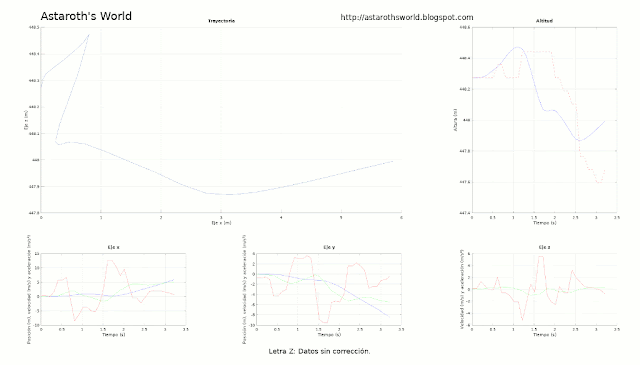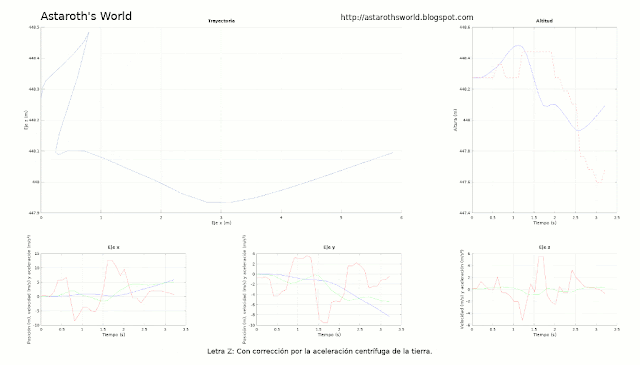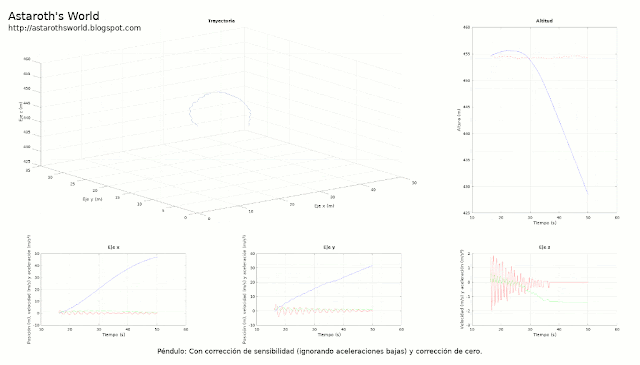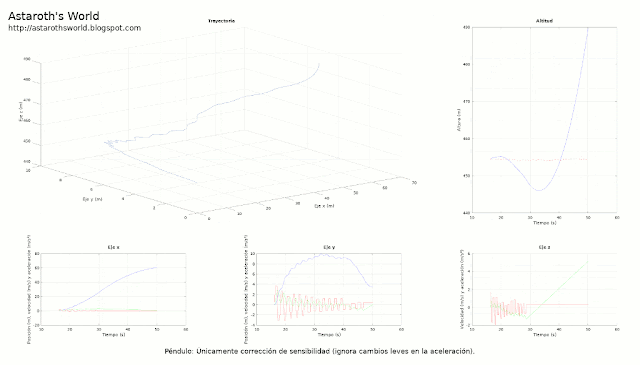Efecto de las distintas correcciones sobre la trayectoria para dos medidas (una "Z" y el oscilar de un péndulo)

Algo parecido, quizás con alguna vuelta de tuerca más, ya lo implementé en la parte IV.

Por otra parte está el problema de las coordenadas. Este problema lo abordé en la parte I, y para este caso he optado por utilizar el sistema de referencia fijado al mundo que te da como opción AndroSensor, aunque creo que lo que hace es aplicar las transformaciones en base a los datos del giróscopo, del que sospecho que es una gran fuente de error. Además, no tengo claro si trabajando en este modo se tiene en cuenta la aceleración centrífuga de la tierra, por lo que la he incluido paramétricamente, de manera que puedo activarla o desactivarla cuando quiera.

Croquis rápido para estimar la aceleración. Coger con pinzas, seguro que hay errores.

La realidad es que esta corrección en el mejor de los casos no cambia mucho las cosas, y en el peor, las estropea, por lo que suelo tenerla desactivada (pensando que a lo mejor ya está incluida en las medidas).

Como comentaba en la entrada anterior sobre AndroSensor, es destacable la cantidad de datos que recopila, incluyendo la latitud (que vemos que vamos a necesitarla en el esquema de arriba), los datos del giróscopo (que sin un cambio automático al sistema de referencia fijado al mundo, los necesitaríamos), la presión (que la voy a usar para esbozar la altitud de forma un poco chapucera), etc.

¿Y para qué voy a utilizar todos estos complejos cálculos? Pues para pintar letritas en el aire con el móvil, y tener una excusa barata para colgar las gráficas en la página (¡qué le vamos a hacer!, tengo debilidad por el subplot).

Sintetizo un poco: voy a pintar letras en el aire con el móvil, y luego voy a intentar reconstruir su posición para obtener lo dibujado.

Muy propio de mi, vamos a empezar por el final. Esto, queridos astarothistas, intentaba ser la letra Z.

Lo primero que vemos es que el orden de magnitud de las distancias es desorbitado: ¡se supone que es una Z de más de 8 metros! Sin embargo, me conformo con que la forma recuerde un poco a la letra, y como bonus, si además se pareciera un poco la altura calculada y la estimada a través de la presión... Esto se ve en la primera gráfica, arriba a la derecha. Hay una línea azul continua (que es la que he calculado integrando la aceleración) y una roja discontinua (que es la que he estimado con la presión). Vemos que, a grandes rasgos, tienen un comportamiento parecido.

Tal y como están las gráficas, vamos construyendo de abajo a arriba: medimos la aceleración (la intentamos corregir), integramos para obtener la velocidad, y volvemos a integrar para sacar la posición.

Al igual que la Z, podemos tener una O:

O pasarnos a las letras griegas, con esta beta y omega:

Y en el raro caso de que las letras no os hubiesen dejado boquiabiertos, os muestro una espectacular medida de la aceleración de un péndulo.

Aunque, como podéis ver en el primer gif, la reconstrucción de la trayectoria es un completo desastre.

¡Seguiré experimentando!